Week 5 Session 1: Introduction to Transformers

Week 5 Session 1: Introduction to Transformers#

Introduction#

In this session, we’ll delve into the Transformer architecture, a groundbreaking model introduced by Vaswani et al. in 2017. Transformers have revolutionized Natural Language Processing (NLP) by effectively capturing long-range dependencies without relying on recurrent or convolutional layers.

Limitations of Traditional RNNs#

Recurrent Neural Networks (RNNs) and their variants like LSTMs and GRUs have been the backbone of sequence modeling tasks. However, they come with several limitations:

  • Sequential Computation: RNNs process sequences step-by-step, making it hard to parallelize computations.

  • Long-Term Dependencies: Difficulty in capturing dependencies that are many time steps apart due to vanishing or exploding gradients.

  • Fixed Context Window: Limited ability to incorporate context from distant tokens effectively.

The Need for Attention Mechanisms#

To overcome these limitations, attention mechanisms were introduced:

  • Parallelization: Attention allows models to process all input tokens simultaneously.

  • Dynamic Context: The model can focus on relevant parts of the input sequence dynamically.

  • Enhanced Long-Range Dependencies: Better at capturing relationships between distant tokens.

Self-Attention Mechanism#

Self-attention, or intra-attention, computes the representation of a sequence by relating different positions within the same sequence.

Scaled Dot-Product Attention#

The core operation in self-attention is the Scaled Dot-Product Attention.

Diagram: Scaled Dot-Product Attention#

Scaled Dot-Product Attention

Figure 1: Scaled Dot-Product Attention mechanism.

Mathematical Formulation#

Given queries \( Q \), keys \( K \), and values \( V \):

\[ \text{Attention}(Q, K, V) = \text{softmax}\left( \frac{Q K^\top}{\sqrt{d_k}} \right) V \]

  • \( Q \): Query matrix

  • \( K \): Key matrix

  • \( V \): Value matrix

  • \( d_k \): Dimension of the key vectors

Code Example: Scaled Dot-Product Attention#

import torch
import torch.nn.functional as F

def scaled_dot_product_attention(Q, K, V):
    d_k = Q.size(-1)
    scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))
    attention_weights = F.softmax(scores, dim=-1)
    return torch.matmul(attention_weights, V), attention_weights

Multi-Head Attention#

Instead of performing a single attention function, the Transformer employs Multi-Head Attention to capture information from different representation subspaces.

Diagram: Multi-Head Attention#

Multi-Head Attention

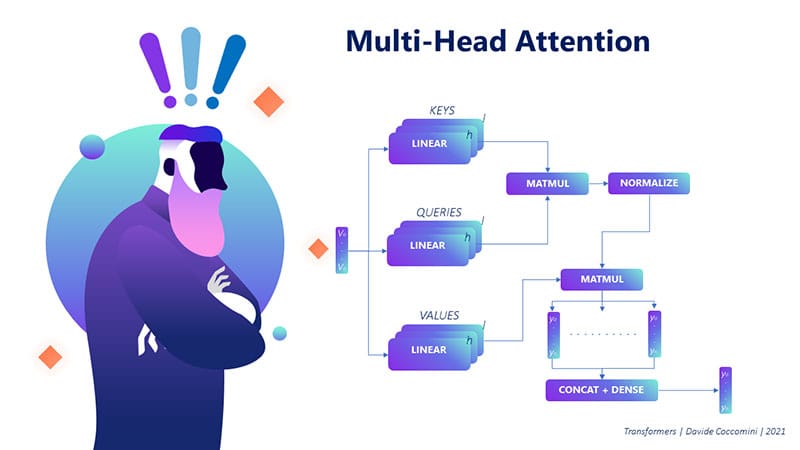
Figure 2: Multi-Head Attention mechanism with multiple attention heads.

Mathematical Formulation#

For each attention head \( i \):

\[ \text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \]

Concatenate all heads:

\[ \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O \]

  • \( W_i^Q, W_i^K, W_i^V \): Parameter matrices for the \( i \)-th head

  • \( W^O \): Output linear transformation matrix

Overview of the “Attention is All You Need” Paper#

Vaswani et al. introduced the Transformer model, which relies entirely on attention mechanisms without any convolutional or recurrent layers.

Key Contributions#

  • Elimination of Recurrence: Enables parallelization and reduces training time.

  • Positional Encoding: Injects information about the relative or absolute position of tokens.

  • Superior Performance: Achieved state-of-the-art results on machine translation tasks.

Dissection of Transformer Components#

Encoder and Decoder Architecture#

The Transformer consists of an encoder and a decoder, each composed of multiple layers.

Diagram: Transformer Architecture#

Transformer Architecture

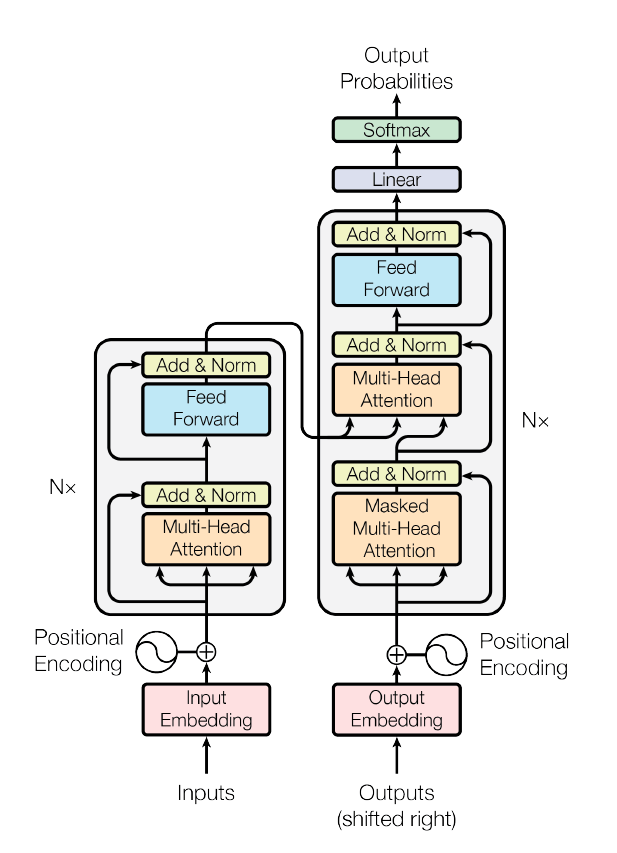
Figure 3: The overall architecture of the Transformer model.

  • Encoder Layers: Each layer has two sub-layers:

    • Multi-Head Self-Attention

    • Position-wise Feed-Forward Network

  • Decoder Layers: Each layer has three sub-layers:

    • Masked Multi-Head Self-Attention

    • Multi-Head Attention over the encoder’s output

    • Position-wise Feed-Forward Network

Positional Encoding#

Since the model has no recurrence, positional encodings are added to the input embeddings to inject sequence order information.

Mathematical Formulation#

For position \( pos \) and dimension \( i \):

\[ \text{PE}_{(pos, 2i)} = \sin\left( \frac{pos}{10000^{2i/d_{\text{model}}}} \right) \]
\[ \text{PE}_{(pos, 2i+1)} = \cos\left( \frac{pos}{10000^{2i/d_{\text{model}}}} \right) \]

Code Example: Positional Encoding#

import torch
import math

def positional_encoding(seq_len, d_model):
    PE = torch.zeros(seq_len, d_model)
    position = torch.arange(0, seq_len).unsqueeze(1)
    div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))
    PE[:, 0::2] = torch.sin(position * div_term)
    PE[:, 1::2] = torch.cos(position * div_term)
    return PE

Feed-Forward Networks#

Applied to each position separately and identically, consisting of two linear transformations with a ReLU activation in between.

Mathematical Formulation#

\[ \text{FFN}(x) = \text{max}(0, x W_1 + b_1) W_2 + b_2 \]

Advantages of Transformers Over Previous Architectures#

  • Parallelization: Allows for efficient use of GPUs.

  • Better at Capturing Long-Range Dependencies: Direct connections between any two positions.

  • Reduced Training Time: Faster convergence due to efficient computations.

  • Scalability: Easily scaled to larger datasets and models.

Conclusion#

The Transformer architecture has set a new standard in NLP by addressing the limitations of traditional RNNs and leveraging attention mechanisms to model sequences more effectively. Understanding each component of the Transformer is crucial for grasping how modern NLP models, including large language models, function.

References#